Problème 1
Soit n un entier strictement positif. Soit T l'ensemble des points
du plan pour lesquels x et y sont des entiers positifs ou nuls et
. Chaque point de T est colorié soit en rouge, soit en bleu. Si un point
est rouge, alors tous les points
de T avec
et
sont rouges. On appelle ensemble de type X un ensemble de n points bleus ayant des abscisses x toutes distinctes, et ensemble de type Y un ensemble de n points bleus ayant des ordonnées y toutes distinctes. Montrer que le nombre d'ensembles de type X est égal au nombre d'ensembles de type Y.
Problème 2
Soit BC un diamètre du cercle
de centre O. Soit A un point de
tel que
. Soit D le milieu de l'arc
ne contenant pas le point C. La droite passant par O parallèle à la droite DA rencontre la droite AC en J. La médiatrice du segment OA rencontre
en E et F. Montrer que J est le centre du cercle inscrit au triangle CEF.
Problème 3
Trouver tous les couples d'entiers
avec
tels qu'il existe une infinité d'entiers a strictement positifs tels que
soit entier.
Problème 4
Soit n un entier strictement plus grand que 1. On note
les diviseurs positifs de n avec
On pose
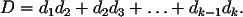
- Montrer que :
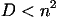
- Trouver tous les entiers n pour lesquels D est un diviseur de
.
Problème 5
Trouver toutes les fonctions
, où
désigne l'ensemble des réels, vérifiant
pour tous les
de
.
Problème 6
Dans le plan, soient
des cercles de rayons 1 avec
. On note respectivement par
leurs centres. On suppose qu'aucune droite ne rencontre plus de deux de ces cercles. Montrer que
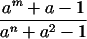
![\[1 = d_1 < d_2 < \ldots < d_k = n.\]](sujets_02_files/sujets_02016.gif)
![\[(f(x) + f(z))(f(y) + f(t)) = f(xy-zt) + f(xt+yz)\]](sujets_02_files/sujets_02022.gif)
![\[\sum^{}_{1\leq i<j\leq n}{1\over
O_iO_j}\leq{(n-1)\pi\over 4}.\]](sujets_02_files/sujets_02028.gif)
